how to find the surface area of a cone
Surface area of a cone
The surface area of a cone can be derived from the surface area of a square pyramid.
Start with a square pyramid and just keep increasing the number of sides of the base. After a very large number of sides, you can see that the figure will eventually look like a cone.This is shown below:
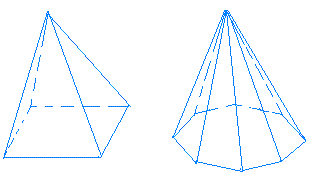
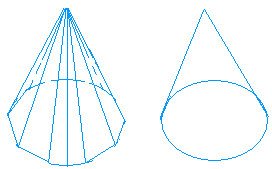
This observation is important because we can use the formula of the surface area of a square pyramid to find that of a cone.
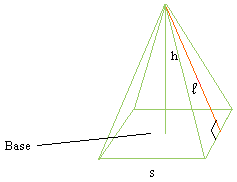
l is the slant height.
The area of the square is s2
The area of one triangle is (s ×
l)/2
Since there are 4 triangles, the area is 4 × (s ×
l)/2 = 2 × s × l
Therefore, the surface area, call it SA is:
SA = s2 + 2 × s ×
l .
Generally speaking, to find the surface area of any regular pyramid where A is the area of the base, the perimeter is P, and the slant height is
l, we use the following formula:
S = A + 1/2 (P × l)
Again A is the area of the base. For a figure with 4 sides, A = s2 with s = length of one side.
Where does the 1/2 (P ×
l) come from?
Let s be the length of the base of a regular pyramid. Then, the area of one triangle is (s ×
l)/2
For n triangles and this also means that the base of the pyramid has n sides, we get ( n × s ×
l)/2
Now P = n × s. When n = 4, of course, P = 4 × s as already shown.
Therefore, after replacing n × s by P, we get S = A + 1/2 (P ×
l)
Let us now use this fact to derive the formula of the surface area of a cone
How to derive the formula to get the surface area of a cone?
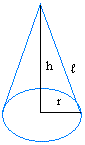
For a cone, the base is a circle, so A = π × r2
P = 2 × π × r
To find the slant height,
l, just use the Pythagorean Theorem
l = r2 + h2
l = √ (r2 + h2)
Putting it all together, we get:
S = A + 1/2 (P ×
l)
S = π × r2 + 1/2 ( 2 × π × r × √ (r2 + h2)
S = π × r2 + π × r × √ (r2 + h2)
3 examples showing how to find the surface area of a cone.
Example #1:
Find the surface area of a cone with a radius of 4 cm, and a height of 8 cm
S = π × r2 + π × r × √ (r2 + h2)
S = 3.14 × 42 + 3.14 × 4 × √ (42 + 82)
S = 3.14 × 16 + 12.56 × √ (16 + 64)
S = 50.24 + 12.56 × √ (80)
S = 50.24 + 12.56 × 8.94
S = 50.24 + 112.28
S = 162.52 cm2
Example #2:
Find the surface area of a cone with a radius of 9 cm, and a height of 12 cm
S = π × r2 + π × r × √ (r2 + h2)
S = 3.14 × 92 + 3.14 × 9 × √ (92 + 122)
S = 3.14 × 81 + 28.26 × √ (81 + 144)
S = 254.34 + 28.26 × √ (225)
S = 254.24 + 28.26 × 15
S = 254.24 + 423.9
S = 678.14 cm2
how to find the surface area of a cone
Source: https://www.basic-mathematics.com/surface-area-of-a-cone.html
Posted by: rodriguenother44.blogspot.com

0 Response to "how to find the surface area of a cone"
Post a Comment